Stationary wavelet transform

The Stationary wavelet transform (SWT)[1] is a wavelet transform algorithm designed to overcome the lack of translation-invariance of the discrete wavelet transform (DWT). Translation-invariance is achieved by removing the downsamplers and upsamplers in the DWT and upsampling the filter coefficients by a factor of 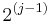2^{(j-1)} in the jth level of the algorithm[2]. The SWT is an inherently redundant scheme as the output of each level of SWT contains the same number of samples as the input – so for a decomposition of N levels there is a redundancy of N in the wavelet coefficients. This algorithm is more famously known as "algorithme à trous" in French (word trous means holes in English) which refers to inserting zeros in the filters. It was introduced by Holdschneider et al.[3]

Contents

Implementation

The following block diagram depicts the digital implementation of SWT.

In the above diagram, filters in each level are up-sampled versions of the previous (see figure below).

Applications

A few applications of SWT are specified below.

Synonyms

The idea of omitting the downsampling in the discrete wavelet transform is sufficiently intuitive that this variant was invented several times with different names.

References

  1. ^ James E. Fowler: The Redundant Discrete Wavelet Transform and Additive Noise, contains an overview of different names for this transform.
  2. ^ Mark J. Shensa, The Discrete Wavelet Transform: Wedding the A Trous and Mallat Algorithms, IEEE Transaction on Signal Processing, Vol 40, No 10, Oct. 1992.
  3. ^ M. Holschneider, R. Kronland-Martinet, J. Morlet and P. Tchamitchian. A real-time algorithm for signal analysis with the help of the wavelet transform. In Wavelets, Time-Frequency Methods and Phase Space, pp. 289–297. Springer-Verlag, 1989.